One of the more powerful features of Argo Navis is its in-built Telescope Pointing Analysis System (TPAS).
Most users will never need it.
However, there are some that do.
The definitive reference to using TPAS is the User Manual in the section on SETUP MNT ERRORS.
See
http://www.wildcard-innovations.com.au/documentation.html
However, sometimes user's ask whether a tutorial is available and I have emailed them this response which appears below.
QUICK TUTORIAL ON TELESCOPE POINTING ANALYSIS SYSTEM FOR DOB OWNERS
There is a reasonable amount to absorb initially but based on working hands-on with many customers, I assure you after a few runs it will become intuitive.
Firstly, I encourage you to spend some time browsing the submenus beneath SETUP MNT ERRORS.
These sub-menus are as follows -
ACQUIRE DATA - switch SAMPLE MODE=ON to enable pointing test sampling
COMPUTE ERRORS - will attempt to fit the pointing model defined in DEFINE MODEL
DEFINE MODEL - used to define which error terms will be fitted by COMPUTE ERRORS
REVIEW DATA - used to examine raw and fitted pointing data residuals along with total raw and fitted RMS. Also allows for deletion of samples.
SET ERROR VALUES - two submenus beneath this -
IN USE NOW - allows one to examine and manually modify mount error terms currently in use by the pointing kernel
SAVED IN NVRAM - allows one to examine and manually modify mount error terms saved in non-volatile memory for later sessions
In a nutshell, you will want to enter your various SETUP parameters as before.
Set DATE/TIME LOCATION as horizon and pole checking is performed.
Highly recommend that you set REFRACTION=ON
If you have an Argo Navis serial port free, have it startup with the navis command before
you begin the pointing test. You will then be able to dump the data for analysis by Wildcard.
In SETUP MNT ERRORS, ACQUIRE DATA, set SAMPLE MODE=ON.
As you will see later, when SAMPLE MODE=ON, a new submenu is enabled when you press ENTER in GUIDE mode.
This new submenu has a selection of DESCRIPTION or SAMPLE MNT ERROR.
When DESCRIPTION appears, if ENTER is pressed, scrolling object description appears as in previous firmware.
When SAMPLE MNT ERROR appears, if ENTER is pressed, object position is sampled.
To preform pointing test, Ideally install reticle or reasonable power eyepiece.
Always center stars as accurately as possible to reduce error.
Perform FIX ALT REF (AUTO ADJUST ON is OK to use) and two-star alignment as before.
Only sample (bright - 6th mag or brighter) stars (ideally those that appear in bright star catalog) or planets.
Use MODE IDENTIFY or MODE TOUR to select a bright star. Suggest start with last alignment star.
When GUIDE appears, press ENTER. When DESCRIPTION appears,
spin DIAL until SAMPLE MNT ERROR appears. Center star/planet in reticle. Press ENTER.
Argo Navis will report pointing residual.
Then suggest sample first alignment star as above.
Sample two more stars. Thus you have so far sampled 4 stars in all.
This is sufficient for you to perform an initial fit.
Go to SETUP MNT ERRORS and select COMPUTE ERRORS.
Press ENTER. Argo Navis will report Root Mean Square (RMS) and Population Standard
Deviation (PSD) of fit. Don't expect any improvement yet. All values are in arc minutes.
Argo Navis will also report IE=XXX where XX.X is the computed value for the fit of the index error in elevation (Alt)
Press ENTER to USE TERM and return to pointing test.
Sample one or two more stars.
Go to SETUP MNT ERROR/DEFINE MODEL and select NON-PERPEN. AXES.
Press ENTER and set NPAE=COMPUTE. Press EXIT twice.
Go to COMPUTE ERRORS. Press ENTER.
Argo Navis will now also attempt to fit for Az to Alt axes not being orthogonal (NPAE).
Take note if RMS and PSD have reduced from before. Take note of standard
deviation of NPAE term (the number after the +/-). Only accept (i.e. USE NOW) if value of term
is at least two or three times larger than its standard deviation.
Acceptance of all terms can also be aborted by pressing EXIT.
Assuming NPAE looks real, press ENTER a few times to accept IE and NPAE as USE NOW.
You can review your pointing test data at any time.
To review pointing data, select REVIEW DATA.
Last sampled point appears as default. Spin DIAL anti-clockwise to view earlier samples.
Large DELTA (triangle) means raw pointing residual.
Spin DIAL fully clockwise until END OF DATA and examine RAW RMS.
Press ENTER and change to DELTAS=FITTED. Press ENTER or EXIT.
Display now shows FIT RMS. Small delta symbol (d) means fitted residual.
Spin DIAL anti-clockwise to examine residuals of samples for the current model in use now.
To delete an item, press ENTER. To delete all items, go to START OF DATA and press ENTER.
Now sample some more stars. Try and take samples with good spread in Alt and Az (i.e. whole sky).
System will not allow to sample star unless 10 degrees above horizon. System will
not allow star to be sampled too close to zenith. Probably best to avoid sampling greater than 85 degrees in Alt.
Use DEFINE MODEL to experiment with other error terms, such as left-right collimation
error (CA) and the two eccentric terms (ECEC and ECES). ECES also accounts for truss tube flexure.
As rule of thumb, probably need about 15 stars with good distribution in Alt to
first characterize CA as it is hard to distinguish from NPAE. Probably need 20 to 100 stars
to more reliably determine NPAE, CA, IE, ECES and ECEC. Suggest always accept IE even if standard
deviation appears larger than value itself.
Think of DEFINE MODE and COMPUTE as a work-bench where you can experiment with
different terms and see if they improve your pointing.
Basically you want to add or remove combinations of terms from within DEFINE MODEL
and then go back and COMPUTE. If the RMS and in particular the PSD does not drop, just press EXIT
and go back to DEFINE MODEL and try again. Normally you will always want to use IE and possibly NPAE.
Sometimes you will also want CA or maybe CA in place of NPAE and maybe ECEC and/or ECES.
If you want to save terms for the next session, never save IE. NPAE, ECEC and ECES are generally
persistent on many mounts and OK to save. CA can vary from session to session with collimation,
eyepieces, etc, so it may not be worth saving. To save terms, when the system gets to the point where
it says USE NOW after pressing ENTER in COMPUTE, you can change USE NOW to USE NOW & SAVE.
During a subsequent observing session you can fix terms line NPAE, ECEC and ECES in
DEFINE MODEL as a constant value. Just spin the DIAL from COMPUTE to the constant value.
By fixing terms, on a subsequent observing run, you can perform a much shorter pointing
run, maybe (4 to 5 stars, which) allows you to nail IE and CA as well as some index error
and tilt terms that are internal to the system but not reported.
As a rule of thumb, if you have 10000 step encoders, that is equivalent to about 2.1' per encoder step.
We have used some mounts where we can get RMS results around 2.1'. In other words, that value
gives you some feel for about as good as you can get when the system becomes encoder resolution
limited. However, we have seen some mounts where the RMS value can be higher, particular if there
are other unmodeled phenomena occurring or non-systematic (i.e. random) behaviour such as the top-end
suddenly moving on the truss poles if it were not tightened properly.
I will also provide here some additional information on the information that is reported to
you whenever you sample a star in GUIDE mode.
Whenever you sample a star, the system will show for 2 seconds how many
stars you have sampled (ITEM= and what the pointing residual was in degrees, arc minutes or arc seconds
for that sample. Like ALIGN mode, you can re-sample if your eye-finger co-ordination was out.
Currently we only allow a star to appear once in the sample data. If you come back
and re-sample, you replace the original datum point.
When you sample a star in GUIDE mode, the delta it reports is always for the current pointing model you have in place.
It you have no pointing model in place, a big DELTA (Greek Triangle=) will be reported.
If you have a pointing model in place, a little delta (Greek d=) will be reported.
The current pointing model is defined by your alignment and whatever values appear in the
SET ERROR VALUES/IN USE NOW MENU.
The nice thing is that when you start the pointing test, before you have fitted a model,
the DELTA reported is your raw pointing. Once you fit a model, the deltas are now those for
when the model is applied. In other words, you start to get some feedback about how your pointing
might be improving (or getting worse) as you sample each new part of the sky. An increasing pointing residual
on a star in some new part of the sky is often a good prompt to go back and COMPUTE again
and update the pointing model.
You can also always use REVIEW DATA to examine the pointing data as both RAW and FITTED.
If when examining FITTED data you notice one sample that sticks out with a very large residual
that you suspect was mis-identified, consider deleting it. Just press ENTER and the ENTER again.
However, don't get "trigger happy" when deleting an item. Sometimes the star might really
have some large pointing residual at it is a glimpse of it telling you that possibly some additional pointing terms
need to be added or something has possibly physically changed.
An introduction to standard deviation and a case study.
The following additional information may be helpful. It was written
in response to a question from a customer who asked about the
significance of the standard deviations Argo Navis reports on each of
the error terms.
It also includes a case study of a pointing test done on a 20" f5 truss pole Dob.
-------------------------------------------------------------------------------------------
The standard deviation gives some measure of the distribution or 'spread'
of data about the mean. Therefore, when a data item has a small standard
deviation, one would expect most of the values to be grouped around the mean.
Thus, we want the standard deviations to be as small as possible.
Suppose your data follows the classic bell shaped curve pattern.
One conceptual way to think about the standard deviation is that it is a measures of how spread out the bell is.
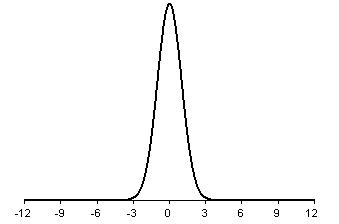
Shown below is a bell shaped curve with a standard deviation of 1.
Notice how tightly concentrated the distribution is.
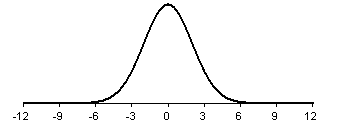
Shown below is a different bell shaped curve, one with a standard deviation of 2.
Notice that the curve is wider, which implies that the data are less concentrated and more spread out.
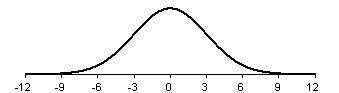
Finally, a bell shaped curve with a standard deviation of 3 appears below.
This curve shows the most spread.
Now let me provide some results from a real telescope, in this case a home-built 20" f5 truss pole Dob.
A pointing test was performed on 30 stars, distributed across the sky.
Though ideally a reticle should be used, in this particular case, no reticle was used, the stars were simply centered in a medium powered eyepiece.
With no terms fitted, the RMS and PSD were as follows -
RMS = 7.5'
PSD = 7.5'
Furthermore, examining the data in REVIEW DATA, the largest raw error on any star
was 16.4'.
When IE and NPAE were fitted the results were as follows -
IE = -0.0' +/- 0.1'
NPAE = +18.5' +/- 1.1'
RMS = 2.2'
PSD = 2.4'
Even though the standard deviation of IE was 0.1, which was larger than its value of 0.0,
we always keep IE.
The value of NPAE looks plausible or 'real' because its value of +18.5' is nearly 17 times
larger than its standard deviation of +/-1.1'
One analogy is to think of a signal (perhaps a radio signal) and then think of noise (perhaps
radio interference or static). Here the +18.5' is the signal and the +/-1.1' is the noise.
We want a large 'signal-to-noise' ratio, which is what we have got.
Now let us attempt to add the term ECES, which can account for a non-centered
Alt axis encoder as well as any tube flexure. The results were as follows -
ECES = +4.4' +/- 1.9'
IE = -3.2' +/- 1.4'
NPAE = 19' +/- 1.0'
RMS = 2.0'
PSD = 2.2'
Notice that the value of ECES is about 2.3 times the value of its standard deviation.
Therefore it looks plausible, but since its signal-to-noise-ratio is low, we would keep
an eye on it. Note how the signal-to-noise on NPAE improved slightly, now 19-to-1.
Also we note that the RMS decreased and most importantly the PSD also decreased.
If the PSD had increased, then the ECES term would probably not be worth keeping.
Notice, by the way, that this mount now has an RMS value that can be considered
close to encoder resolution limited. An excellent result. A quick examination of
the fitted error value residuals in REVIEW DATA also showed that the largest
error on any star had dropped to 3.7'. In fact, further examination showed that
the star that originally showed the largest raw pointing error of 16.4' dropped
down to 20" once fitted!
To continue with this case study, could the overall RMS/PSD be improved further
by adding another term? Let us try adding ECEC. The results we get are -
ECEC = +5.4' +/- 5.3'
ECES = +9.4' +/- 6.1'
IE = -10.1' +/- 8.1'
NPAE = 18.9' +/- 1.0'
RMS = 2.0'
PSD = 2.3'
Note how the signal-to-noise ratio of the new term, ECEC, is very low, nearly 1:1.
This tells us that ECEC doesn't look plausible. Other clues include the fact that the standard
deviations of some of the other terms increased and the PSD also increased.
Therefore, we would reject ECEC.
Finally, let us try and use CA. The results we get are -
CA = 7.7' +/- 8.1'
ECES = 4.4' +/- 1.9'
IE = -3.2' +/- 1.4'
NPAE = +13.3' +/- 6.1'
RMS = 2.0'
PSD = 2.2'
Note how the standard deviation of the CA term is greater than CA itself. It looks like
it is all noise. Notice also how the signal-to-noise ratio of NPAE also worsened to 2.2'.
The RMS and PSD values also did not improve. Adding CA therefore looks as if it
doesn't help and in fact possibly worsens the statistical integrity of the model.
If the pointing test had been extended to include more stars, particularly some additional
stars with altitudes in the range 60 to 80 degrees, it might then have been worth
trying to fit a model using CA again as it may come out of the 'noise'.
Another experiment with the above data is to remove NPAE and just use CA.
The results were as follows -
CA = 25.3' +/- 1.5'
ECES = 4.2' +/- 1.5'
IE = 3.1' +/- 1.5'
RMS = 2.1'
PSD = 2.4'
This model also looks plausible. However, notice that the RMS and PSD values increased
compared to just using NPAE instead of CA. The reason CA could be substituted for NPAE
in this manner to still get a reasonable fit is that the characteristic 'signature' of CA and NPAE
are very similar. Statisticians would say that CA and NPAE are 'highly correlated'.
In fact, we know from additional analysis of this particular data that these two terms have nearly
a 99% correlation in this instance. Therefore, it is probably best to use either NPAE or CA but not both
inthis particular case.
So how does one determine whether the mount's error is NPAE or CA? As mentioned above,
the number of pointing test samples would need to be increased, in particular selecting stars
over a greater range of altitudes, particularly more stars at higher altitudes, in order to 'unravel' the
NPAE and CA terms.
Based on further tests of this particular telescope, it looks as if the NPAE term of
around +19.0' is real and reasonably persistent. That and the ECES value of 4.4' were
saved and used in subsequent observing sessions. On these subsequent runs, the user
performed a short pointing run of typically 4 to 5 stars. In DEFINE MODEL they had -
ECES = +4.4'
IE = COMPUTE
NPAE = 19.0'
After performing a COMPUTE and then accepting the model, they were able to
achieve close to encoder resolution limited whole-sky pointing for the rest of the night.
Hopefully the above is helpful to you, the reader.
Think of the DEFINE MODEL and COMPUTE ERRORS menus as a laboratory workbench
where you can hypothesize what the error terms might be in DEFINE MODEL and
then determine their fit in COMPUTE ERRORS. Remember when you can hit EXIT at
any time in COMPUTER ERRORS which will cancel accepting the terms. Typically
a user will go back and forth between DEFINE MODEL and COMPUTE ERRORS in
this fashion, experimenting with various terms.
When performing a pointing test, we recommend to recompute the model often and then
accept it, as it can assist in locating further stars during the pointing test run.
After a while, you will begin to become familiar with the types of values your particular mount produces.
![[Logo]](/forum/templates/default/images/logo.jpg)